Contents
▶ 동역학을 다루는 포스팅
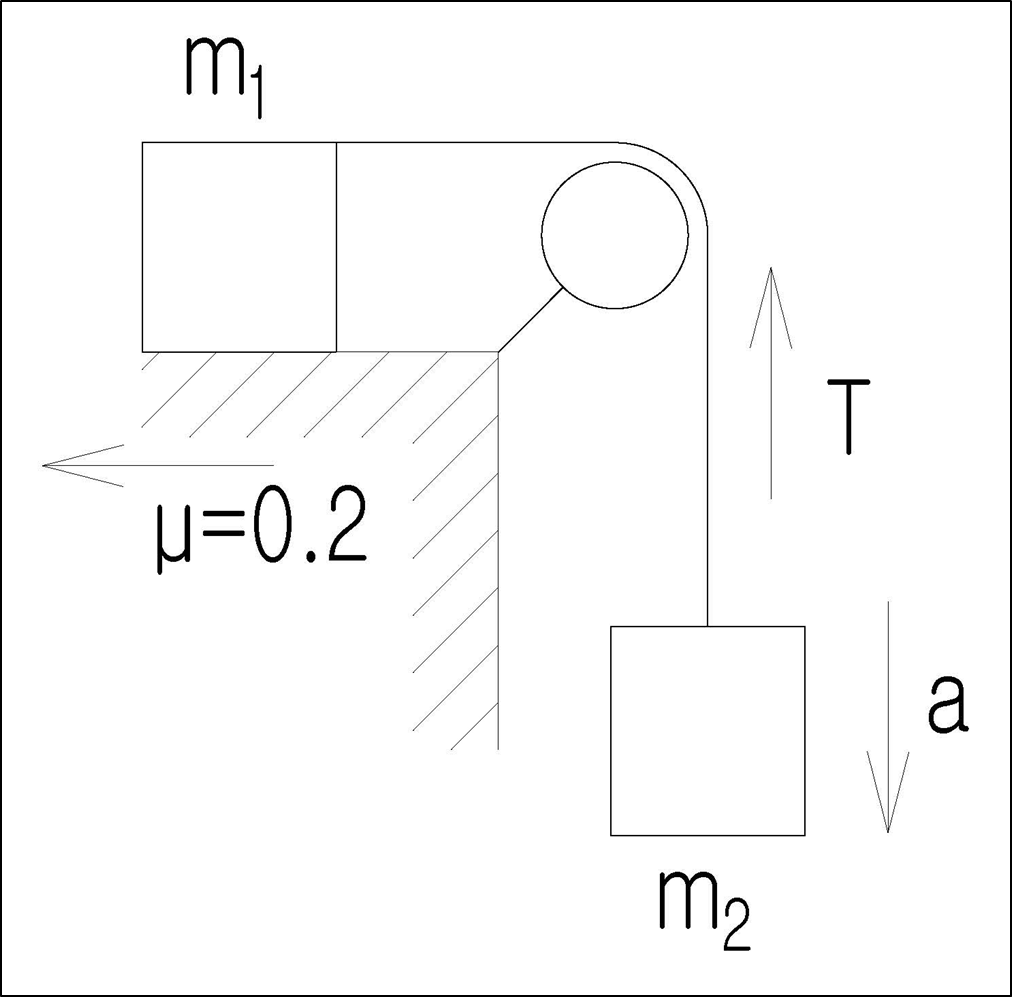
고정도르래
줄의 가속도 \( \vec{a} = \frac{(m_{2} – m_{1})}{m1 + m2} \cdot g \)
줄에 걸리는 장력 \( \vec{T} = \frac{(2m_{1} \cdot m_{2})}{m_{1} + m_{2}} \cdot g \)
\( f_{1} = \mu N \)
3. 구속된 운동의 운동방정식
구속된 운동의 운동 방정식은 물체가 특정 구속조건 하에서 어떻게 운동하는지를 정량적으로 설명합니다. 이 섹션에서는 라그랑주 방정식을 통한 운동 방정식의 유도, 운동량 보존, 그리고 에너지 보존의 관점에서 구속된 운동을 분석합니다.
3.1) 라그랑주 방정식의 도입
라그랑주 방정식은 구속된 시스템에서 운동의 방정식을 유도하는 효율적인 방법을 제공합니다. 이 방정식은 시스템의 운동 에너지와 위치 에너지를 통해 정의된 라그랑지안 함수를 사용합니다.
- 라그랑주 방정식: \( \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_i}\right) – \frac{\partial L}{\partial q_i} = 0 \)
- 여기서 L=T−V는 라그랑지안(운동 에너지 T에서 위치 에너지 V를 뺀 값), \( q_{i} \)는 일반화된 좌표, \( \dot{q}_{i} \)는 일반화된 속도입니다.
3.2) 운동량 보존과 구속된 운동
구속된 시스템에서도, 운동량 보존의 법칙이 적용될 수 있습니다. 이는 특히 외부 힘이 없는 폐쇄된 시스템에서 중요합니다.
3.3) 구속된 운동에서의 에너지 보존
에너지 보존법칙은 구속된 운동에서도 유효합니다. 시스템의 총 에너지(운동 에너지와 위치 에너지의 합)는 외부에서 에너지가 가해지거나 제거되지 않는 한 일정합니다.
예제 문제 및 풀이
예제 1
문제: 길이가 l인 단순 펜듈럼의 운동 방정식을 라그랑주 방정식을 사용하여 유도하세요.
풀이:
펜듈럼의 운동 에너지 T와 위치 에너지 V는 각각 다음과 같습니다.
- 운동 에너지: \( T = \frac{1}{2}ml^2\dot{\theta}^2 \)
- 위치 에너지: \( V = mgl(1 – \cos{\theta}) \)
라그랑지안 L=T−V는 다음과 같습니다.
\( L = \frac{1}{2}ml^2\dot{\theta}^2 – mgl(1 – \cos{\theta}) \)
라그랑주 방정식을 적용하여,
\( \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta}}\right) – \frac{\partial L}{\partial \theta} = 0 \)
이를 풀면,
\( ml^2\ddot{\theta} + mgl\sin{\theta} = 0 \)
이는 단순 펜듈럼의 운동 방정식입니다.
예제 2
문제: 반지름 R의 원형 궤도 위를 질량 m인 물체가 속도 v로 원운동하고 있습니다. 이 시스템의 라그랑지안을 구하고, 구속력을 계산하세요.
풀이:
원운동에서 물체의 운동 에너지 �T는 다음과 같습니다.
\( T = \frac{1}{2}mv^2 \)
원운동에서 위치 에너지 V는 변하지 않으므로,
\( V = 0 \)
라그랑지안 L=T−V는,
\( L = \frac{1}{2}mv^2 \)
구속력 \( F_{c} \)는 구심력으로, 라그랑지안에서 직접 계산할 수 없으나, 구심력의 정의를 사용하여,
\( F_c = m\frac{v^2}{R} \)
를 얻을 수 있습니다.
다른 동역학 링크