Contents
▶ 고체역학에서 응력(Stress)에 다루는 포스팅
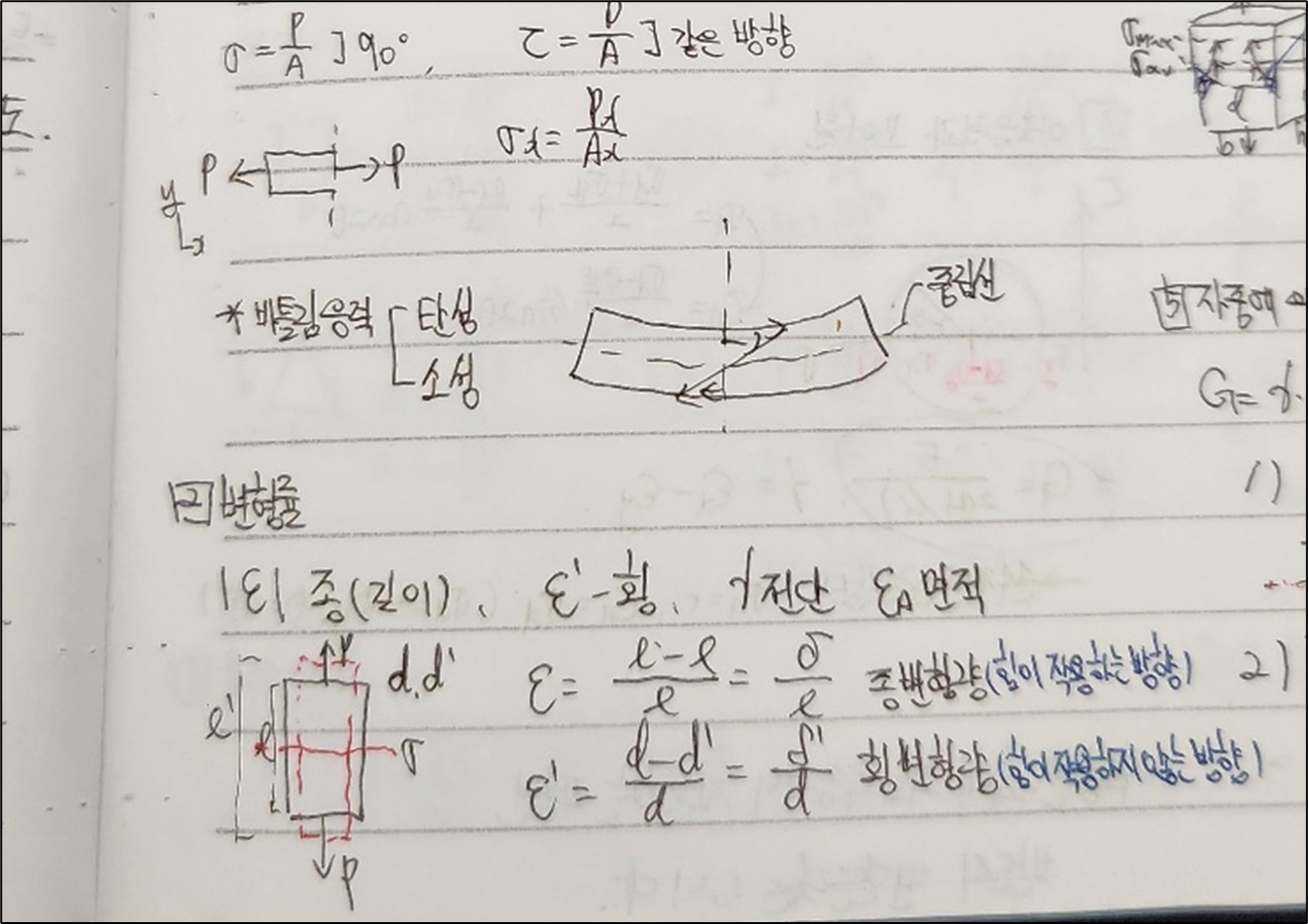
Section 01) 응력과 변형률
1. 서론: 응력과 변형률의 기초
1) 응력(Stress)이란 무엇인가?
응력은 단위 면적당 작용하는 힘으로, 외부로부터의 힘에 대한 재료의 내부 저항을 나타냅니다. 응력의 기본 단위는 파스칼(Pa)이며, 수학적으로 다음과 같이 표현됩니다:
\( σ = \frac{F}{A} \)
여기서:
- σ는 응력,
- F는 재료에 작용하는 힘,
- A는 힘이 작용하는 면적입니다.
응력은 재료의 강도와 변형을 결정하는 중요한 요소입니다.
2) 변형률(Strain)의 정의
변형률은 재료가 받는 응력에 의해 발생하는 단위 길이당 변형의 정도를 나타냅니다. 변형률은 차원이 없는 수치로, 다음과 같이 정의됩니다:
\( \epsilon = \frac{\Delta L}{L_0} \)
여기서:
- ϵ은 변형률,
- ΔL은 길이의 변화,
- \( L_{0} \)은 원래 길이입니다.
변형률은 재료가 얼마나 쉽게 변형되는지를 나타내며, 재료의 유연성과 연관이 있습니다.
3) 응력과 변형률의 기본 개념
| 용어 | 기호 | 정의 | 단위 |
|---|---|---|---|
| 응력 | σ | 단위 면적당 작용하는 힘 | 파스칼 (Pa) |
| 변형률 | ε | 단위 길이당 변형의 정도 | 없음 (차원 없음) |
4) 연습문제
문제 1
문제: 길이가 3m인 알루미늄 막대가 5000N의 힘을 받고 있습니다. 막대의 단면적이 0.01 \( m^{2} \)일 때, 막대에 발생하는 응력을 계산하십시오.
풀이: 응력은 힘과 단면적의 비율로 계산됩니다.
\( \sigma = \frac{F}{A} \)
\( \sigma = \frac{5000N}{0.01m^{2}} = 500,000Pa \)
문제 2
문제: 위의 알루미늄 막대가 0.004m 만큼 늘어났다면, 변형률은 얼마입니까?
풀이: 변형률은 길이 변화와 원래 길이의 비율로 계산됩니다.
\( \epsilon = \frac{\Delta L}{L_{0}} \)
\( \epsilon = \frac{0.004m}{3m} \approx 0.00133 \)
2. 응력의 종류
1) 축응력 (Axial Stress)
축응력은 재료의 축을 따라 작용하는 응력으로, 재료가 늘어나거나 줄어드는 힘에 의해 발생합니다. 수학적으로 축응력은 다음과 같이 표현됩니다:
\( \sigma_{\text{axial}} = \frac{F_{\text{axial}}}{A} \)
여기서 \( σ_{axial} \)는 축응력, \( F_{axial} \)는 축 방향으로 작용하는 힘, A는 단면적입니다.
2) 전단응력 (Shear Stress)
전단응력은 재료의 한 면을 다른 면에 대해 평행하게 밀어내는 힘에 의해 발생합니다. 전단응력은 다음과 같이 정의됩니다:
\( \tau = \frac{F_{\text{shear}}}{A} \)
여기서 τ는 전단응력, \( F_{shear} \)는 전단 힘, A는 전단이 작용하는 면적입니다.
3) 체적응력 (Volumetric Stress)
체적응력은 재료 전체에 균일하게 작용하는 압력으로 인해 발생하며, 주로 압축 상태에서 논의됩니다. 체적응력은 다음과 같이 표현됩니다:
\( \sigma_{\text{volumetric}} = -p \)
여기서 \( σ_{volumetric} \)는 체적응력, p는 압력을 나타냅니다.
4) 표: 응력의 종류
| 응력의 종류 | 기호 | 수식 | 설명 |
|---|---|---|---|
| 축응력 (Axial Stress) | \( σ_{axial} \) | \( σ_{axial} = \frac{F_{axial}}{A} \) | 재료의 축을 따라 작용하는 응력 |
| 전단응력 (Shear Stress) | τ | \( τ = \frac{F_{shear}}{A} \) | 재료의 면을 평행하게 밀어내는 응력 |
| 체적응력 (Volumetric Stress) | \( σ_{volumetric} \) | \( σ_{volumetric} = -p \) | 재료 전체에 균일하게 작용하는 압력에 의한 응력 |
5) 연습문제
문제 1
문제: 단면적이 0.05 \( m^{2} \)인 강철 기둥에 25000N의 축 방향 힘이 작용하고 있습니다. 기둥에 발생하는 축응력을 계산하십시오.
풀이: 축응력은 힘과 단면적의 비율로 계산됩니다.
\( \sigma_{\text{axial}} = \frac{F_{\text{axial}}}{A} \)
\( \sigma_{\text{axial}} = \frac{25000N}{0.05 m^2} = 500,000 Pa \)
문제 2
문제: 너비가 0.3m이고 높이가 0.2m인 판에 6000N의 전단력이 작용하고 있습니다. 판에 발생하는 전단응력을 계산하십시오.
풀이: 전단응력은 전단력과 작용 면적의 비율로 계산됩니다.
\( \tau = \frac{F_{\text{shear}}}{A} \)
\( \tau = \frac{6000N}{0.3m \times 0.2m} = 100,000 Pa \)

3. 변형률의 종류
1) 선형 변형률 (Linear Strain)
선형 변형률은 재료의 길이 변화에 따른 변형률을 나타냅니다. 이는 원래 길이에 대한 변형된 길이의 비율로 계산됩니다. 선형 변형률의 수식은 다음과 같습니다:
\( \epsilon_{\text{linear}} = \frac{\Delta L}{L_0} \)
여기서 \( \epsilon_{\text{linear}} \)는 선형 변형률, ΔL은 길이의 변화, \( L_{0} \)는 원래 길이입니다.
2) 전단 변형률 (Shear Strain)
전단 변형률은 재료의 각 변형을 나타냅니다. 이는 두 면이 서로에 대해 이동한 각도로 정의됩니다. 전단 변형률의 수식은 다음과 같습니다:
\( \gamma = \tan(\phi) \)
여기서 γ는 전단 변형률, ϕ는 변형된 각도입니다.
3) 체적 변형률 (Volumetric Strain)
체적 변형률은 재료의 전체 체적 변화를 나타냅니다. 이는 원래 체적에 대한 변형된 체적의 비율로 표현됩니다. 체적 변형률의 수식은 다음과 같습니다:
\( \epsilon_{\text{volumetric}} = \frac{\Delta V}{V_0} \)
여기서 \( \epsilon_{\text{volumetric}} \)는 체적 변형률, ΔV는 체적의 변화, \( V_{0} \)는 원래 체적입니다.
4) 표: 변형률의 종류
| 변형률의 종류 | 기호 | 수식 | 설명 |
|---|---|---|---|
| 선형 변형률 (Linear Strain) | \( \epsilon_{\text{linear}} \) | \( \epsilon_{\text{linear}} = \frac{\Delta L}{L_0} \) | 길이 변화에 따른 변형률 |
| 전단 변형률 (Shear Strain) | γ | \( \gamma = \tan(\phi) \) | 각 변형에 따른 변형률 |
| 체적 변형률 (Volumetric Strain) | \( \epsilon_{\text{volumetric}} \) | \( \epsilon_{\text{volumetric}} = \frac{\Delta V}{V_0} \) | 전체 체적 변화에 따른 변형률 |
5) 연습문제
문제 1
문제: 원래 길이가 2m인 막대가 0.006m 늘어났습니다. 이 막대의 선형 변형률을 계산하십시오.
풀이: 선형 변형률은 길이 변화와 원래 길이의 비율로 계산됩니다.
\( \epsilon_{\text{linear}} = \frac{\Delta L}{L_0} \)
\( \epsilon_{\text{linear}} = \frac{0.006m}{2m} = 0.003 \)
문제 2
문제: 한 변이 0.4m인 정사각형 판이 전단력에 의해 한 변이 0.005m만큼 이동했습니다. 전단 변형률을 계산하십시오.
풀이: 전단 변형률은 변형 각도로 계산됩니다.
\( \gamma = \tan^{-1}\left(\frac{\Delta x}{L}\right) \)
\( \gamma = \tan^{-1}\left(\frac{0.005m}{0.4m}\right) \approx 0.0125 \text{ rad} \)

4. 응력-변형률 관계
1) 훅의 법칙 (Hooke’s Law)
훅의 법칙은 탄성 범위 내에서 응력과 변형률이 비례 관계에 있다는 것을 설명합니다. 이 법칙은 다음과 같이 표현됩니다:
\( \sigma = E \cdot \epsilon \)
여기서:
- σ는 응력,
- E는 탄성계수 (Modulus of Elasticity),
- ϵ는 변형률입니다.
이 수식은 재료가 탄성 한계 내에서 변형될 때 적용됩니다.
2) 탄성계수 (Modulus of Elasticity)
탄성계수는 재료의 탄성 거동을 나타내는 물리적 상수로, 재료가 받는 응력에 대한 변형률의 비율을 나타냅니다. 탄성계수는 훅의 법칙에서 E로 표현됩니다.
3) 전단 탄성계수 (Modulus of Rigidity)
전단 탄성계수는 재료의 전단 변형에 대한 저항력을 나타내는 물리적 상수입니다. 전단응력과 전단 변형률 사이의 관계는 다음과 같이 표현됩니다:
\( \tau = G \cdot \gamma \)
여기서:
- τ는 전단응력,
- G는 전단 탄성계수 (Modulus of Rigidity),
- γ는 전단 변형률입니다.
4) 표: 응력-변형률 관계
| 개념 | 기호 | 수식 | 설명 |
|---|---|---|---|
| 훅의 법칙 (Hooke’s Law) | σ, ϵ | σ=E⋅ϵ | 탄성 범위 내에서 응력과 변형률의 비례 관계 |
| 탄성계수 (Modulus of Elasticity) | E | – | 재료의 탄성 거동을 나타내는 물리적 상수 |
| 전단 탄성계수 (Modulus of Rigidity) | G | τ=G⋅γ | 재료의 전단 변형에 대한 저항력을 나타내는 물리적 상수 |
5) 연습문제
문제 1
문제: 탄성계수가 200 GPa인 재료에서 0.002의 변형률이 발생했습니다. 이 재료에 발생하는 응력을 계산하십시오.
풀이: 훅의 법칙에 따라 응력을 계산합니다.
\( \sigma = E \cdot \epsilon \)
\( \sigma = 200 \times 10^9 Pa \times 0.002 = 400 MPa \)
문제 2
문제: 전단 탄성계수가 80 GPa인 재료에서 전단 변형률이 0.0015 발생했습니다. 이 재료에 발생하는 전단응력을 계산하십시오.
풀이: 전단응력은 전단 탄성계수와 전단 변형률을 곱하여 계산됩니다.
\( \tau = G \cdot \gamma \)
\( \tau = 80 \times 10^9 Pa \times 0.0015 = 120 MPa \)
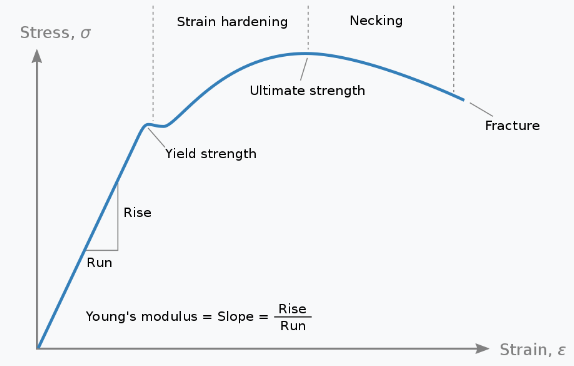
5. 응력-변형률 곡선
1) 탄성 범위 (Elastic Range)
탄성 범위는 재료가 외부 힘을 제거한 후 원래 상태로 복원될 수 있는 응력 범위를 나타냅니다. 이 범위에서 재료의 거동은 훅의 법칙에 따라 설명됩니다. 탄성 범위 내의 응력과 변형률 관계는 다음과 같이 표현됩니다:
\( \sigma = E \cdot \epsilon \)
여기서 σ는 응력, E는 탄성계수, ϵ는 변형률입니다.
2) 항복점 (Yield Point)
항복점은 탄성 범위를 넘어선 후 재료가 영구적 변형을 시작하는 응력 수준입니다. 항복점을 넘어서면 재료는 탄성 범위로 돌아가지 않습니다. 항복점은 특정한 수치로 정의되며, 재료의 유형에 따라 다릅니다.
3) 소성 범위 (Plastic Range)
소성 범위는 재료가 영구적 변형을 경험하는 응력 범위입니다. 이 범위에서는 재료가 더 이상 탄성 거동을 보이지 않으며, 변형된 상태에서 멈춥니다.
4) 파단 (Fracture)
파단은 재료가 결국 파손되는 지점을 나타냅니다. 파단점에서는 재료가 더 이상 하중을 견디지 못하고 끊어지거나 분리됩니다.
5) 표: 응력-변형률 곡선의 주요 특징
| 특징 | 설명 |
|---|---|
| 탄성 범위 | 재료가 외부 힘을 제거한 후 원래 상태로 복원될 수 있는 범위 |
| 항복점 | 탄성 범위를 넘어서 영구적 변형이 시작되는 응력 수준 |
| 소성 범위 | 재료가 영구적 변형을 경험하는 응력 범위 |
| 파단 | 재료가 하중을 견디지 못하고 끊어지거나 분리되는 지점 |
6) 연습문제
문제 1
문제: 특정 강철의 항복점이 250 MPa입니다. 이 강철의 탄성계수가 200 GPa일 때, 항복점에서의 변형률을 계산하십시오.
풀이: 항복점에서의 변형률은 훅의 법칙을 이용하여 계산됩니다.
\( \epsilon = \frac{\sigma}{E} \)
\( \epsilon = \frac{250 \times 10^6 Pa}{200 \times 10^9 Pa} = 0.00125 \)
문제 2
문제: 파단 강도가 500 MPa인 재료의 탄성계수가 100 GPa일 때, 파단점에서의 변형률을 계산하십시오.
풀이: 파단점에서의 변형률을 계산합니다. (참고로 실제 파단점에서는 훅의 법칙이 적용되지 않을 수 있습니다.)
\( \epsilon = \frac{\sigma}{E} \)
\( \epsilon = \frac{500 \times 10^6 Pa}{100 \times 10^9 Pa} = 0.005 \)
6. 열응력 (Thermal Stress)
1) 온도 변화에 의한 응력
열응력은 재료가 온도 변화로 인해 발생하는 응력입니다. 온도가 변할 때, 재료는 팽창하거나 수축하려는 경향이 있으며, 이러한 변화가 제약을 받을 때 열응력이 발생합니다. 열응력의 수식은 다음과 같습니다:
\( \sigma_{\text{thermal}} = E \cdot \alpha \cdot \Delta T \)
여기서:
- \( \sigma_{\text{thermal}} \)는 열응력,
- E는 재료의 탄성계수,
- α는 재료의 열팽창 계수,
- ΔT는 온도 변화입니다.
2) 열팽창 계수 (Coefficient of Thermal Expansion)
열팽창 계수는 재료가 온도 변화에 따라 얼마나 팽창하거나 수축하는지를 나타내는 상수입니다. 다음과 같이 정의됩니다:
\( \alpha = \frac{\Delta L / L_0}{\Delta T} \)
여기서:
- α는 열팽창 계수,
- ΔL는 길이 변화,
- \( L_{0} \)는 원래 길이,
- ΔT는 온도 변화입니다.
3) 표: 열응력과 열팽창 계수
| 개념 | 기호 | 수식 | 설명 |
|---|---|---|---|
| 열응력 (Thermal Stress) | \( \sigma_{\text{thermal}} \) | \( \sigma_{\text{thermal}} = E \cdot \alpha \cdot \Delta T \) | 온도 변화로 인해 발생하는 재료 내의 응력 |
| 열팽창 계수 (Coefficient of Thermal Expansion) | α | \( \alpha = \frac{\Delta L / L_0}{\Delta T} \) | 온도 변화에 따른 재료의 팽창 또는 수축 비율 |
4) 연습문제
문제 1
문제: 탄성계수가 70 GPa이고, 열팽창 계수가 24×10−624×10−6 /°C인 알루미늄 막대가 40°C 증가했습니다. 열응력을 계산하십시오.
풀이: 열응력을 계산합니다.
\( \sigma_{\text{thermal}} = E \cdot \alpha \cdot \Delta T \)
\( \sigma_{\text{thermal}} = 70 \times 10^9 Pa \times 24 \times 10^{-6} / \text{°C} \times 40 \text{°C} = 67.2 MPa \)
문제 2
문제: 길이가 2m인 철제 막대가 30°C 온도 변화를 겪었습니다. 철의 탄성계수가 200 GPa이고, 열팽창 계수가 12×10−612×10−6 /°C일 때, 발생하는 열응력을 계산하십시오.
풀이: 열응력을 계산합니다.
\( \sigma_{\text{thermal}} = E \cdot \alpha \cdot \Delta T \)
\( \sigma_{\text{thermal}} = 200 \times 10^9 Pa \times 12 \times 10^{-6} / \text{°C} \times 30 \text{°C} = 72 MPa \)
다른 기계 가공법 링크